Guest Post by Willis Eschenbach
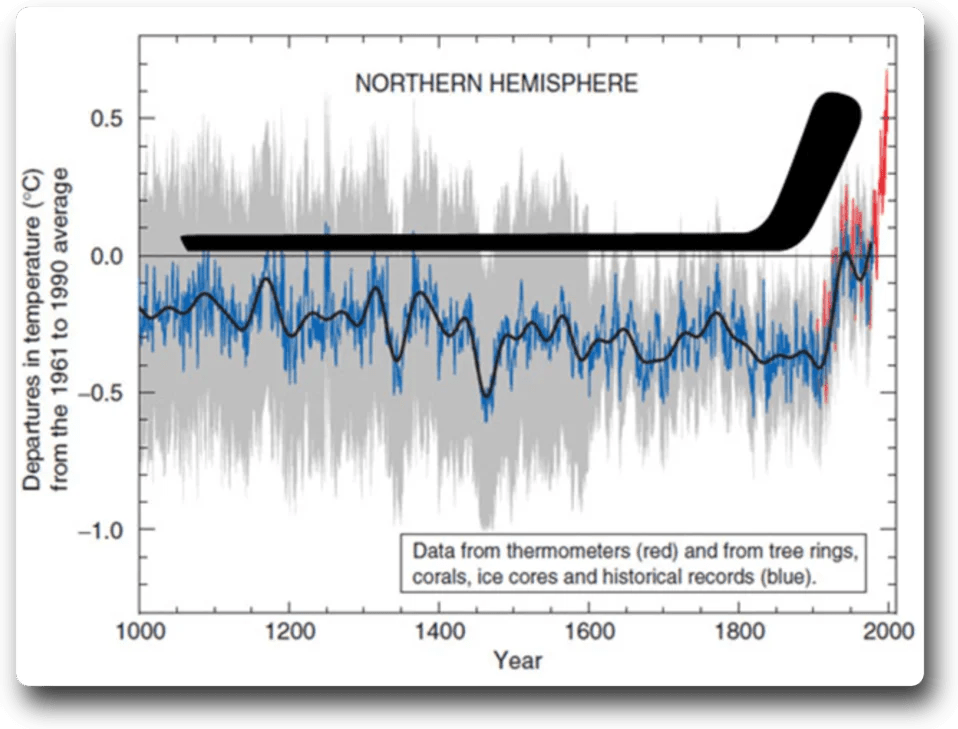
The iconic “hockeystick” simply refuses to die. It was first created by Mann, Bradley and Hughes in their 1998 paper Global-scale temperature patterns and climate forcing over the past six centuries (hereinafter “MBH98”).
Figure 1. Original hockeystick graph
MBH98 claimed to show that after a long period with very little change, suddenly the world started warming, and warming fast.
Back a couple of decades ago, Steve McIntyre over at Climate Audit did yeoman work in discovering a host of errors in MBH98. And somewere in that time, someone, likely Steve but perhaps not, noted that the curious (and mathematically incorrect) procedure used in MBH98 could actively mine hockeysticks out of red noise.
Despite all of that, MBH was succeeded by various of what I call “hockalikes”, studies that purported to independently find a hockeystick in the historical record and thus were claimed to support and validate the original MBH98 hockeystick.
Of course, these repeated many of the same errors as had been exposed by McIntyre and others. Here is the money graphic from my post Kill It With Fire, which analyzed the Mann 2008 attempt to rehabilitate the hockeystick (M2008).

Figure 2. Cluster dendrogram showing similar groups in the proxies of the M2008 hockalike
Note that the hockeystick shape depends on only a few groups of proxies.
Now, what I realized a few days ago was that although I’d believed that the MBH98 incorrect math could mine hockeysticks out of red noise, I’d never tried it myself. And more to the point, I’d never tried it with simpler math, straight averages instead of the uncentered principal components method of MBH98. So this is basically my lab notebook from that investigation.
The most expansive of these hockalikes involve the PAGES dataset, which has had three incarnations—PAGES2017, PAGES2019, and PAGES2K. PAGES2K starts in the year 1AD and contains 600+ proxy records. Here are several PAGES2K reconstructions, from a Nature article promoting the claim that there is “Consistent multidecadal variability in global temperature reconstructions and simulations over the Common Era“

Figure 3. Several historical reconstructions using the PAGES2K dataset.
Now, as Figure 3 shows, it’s true that several different investigations done by different teams have yielded very similar hockeystick shapes. While this seems to greatly impress the scientists, this post will show why that is both true and meaningless.
To do that, first we need to understand the steps in the process of creating proxy-based historical temperature reconstructions. A “proxy” is some measurement of differences in some measurable variable that changes with the temperature. For example, in general when it is warmer, both trees and coral grow faster. Thus, we can analyze the widths of their annual rings as a proxy for the surrounding temperature. Other temperature proxies are isotopes in ice cores, sediment rates in lakes, speleothems, magnesium/calcium ratios in seashells, and the like.
The process of creating a proxy-based historical dataset goes like this:
- Gather a bunch of proxies.
- Discard the ones that are not “temperature sensitive”. Temperature-sensitive proxies can be identified by seeing if they vary in general lockstep (or anti-lockstep) with historical temperature observation (high correlation).
- They might be positively correlated (both temperature and the proxy go up/down together) or negatively correlated (when one goes up the other goes down). Either one is sensitive to the temperature and thus, is useful. So we need to simply flip over the proxies with negative correlation.
- Use some mathematical method, simple or complex, to average all or some subset of the individual proxies.
- Declare success.
Seems like a reasonable idea. Find temperature-sensitive proxies, and average them in some fashion to reconstruct the past. So … what’s not to like?
To start with, here’s the description from the paper announcing the PAGES2K, entitled A global multiproxy database for temperature reconstructions of the Common Era.
Reproducible climate reconstructions of the Common Era (1 CE to present) are key to placing industrial-era warming into the context of natural climatic variability.
Here we present a community-sourced database of temperature-sensitive proxy records from the PAGES2k initiative. The database gathers 692 records from 648 locations, including all continental regions and major ocean basins. The records are from trees, ice, sediment, corals, speleothems, documentary evidence, and other archives. They range in length from 50 to 2000 years, with a median of 547 years, while temporal resolution ranges from biweekly to centennial. Nearly half of the proxy time series are significantly correlated with HadCRUT4.2 surface temperature over the period 1850–2014.
So PAGES2K has completed the first step of creating a proxy-based temperature reconstruction. They’ve gathered a host of proxies, and they’ve noted that about half of them are “temperature sensitive” based on their agreement with the HadCRUT surface temperature.
Again … what’s not to like?
To demonstrate what’s not to like, I created groups of 692 “pseudoproxies” to match the size of the PAGES2K dataset. These are randomly generated imitation “time series” starting in the Year 1, to match the length of the PAGES2K. I created them so their autocorrelation roughly matched the autocorrelation of the temperature records, which is quite high. That way they are “lifelike”, a good match for actual temperature records. Here are the first ten of a random batch.

Figure 4. Randomly generated pseudoproxies with high autocorrelation, also called “red noise”.
As you can see, all of them could reasonably represent the two-millennia temperature history of some imaginary planet. How good is their correlation with temperature observations? Figure 4 shows that data.

Figure 5. Correlations of 692 random pseudoproxies with the Berkeley Earth modern temperature observations.
This is about what we’d expect, with approximately half of the pseudoproxies having a positive correlation with the observational temperature data, the other half with a negative correlation, and most of the proxies not having a strong correlation with the temperature.
And here’s the average of all of the pseudoproxies.

Figure 6. Average, 692 pseudoproxies. The red line shows the start of the Berkeley Earth instrumental record. Note that there is no hockeystick—to the contrary, in this case, to avoid biasing my results, I’ve chosen a batch of pseudoproxies whose average goes down at the recent end. Nor is there any significant trend in the overall data.
OK, so we have the proxies, and we’ve calculated the correlation of each one with the instrumental record. Then, following Step 3 in the procedure outlined above, I flipped over those proxies which had a negative correlation to the instrumental record. That meant all the proxies were positively correlated with the Berkeley Earth data.
At this point, I was going to see what an average would look like if I selected only the pseudoproxies with a high correlation with the instrumental record, say 0.5 or more … but before that, for no particular reason, I thought I’d look at a bozo-simple average of the whole dataset. Color me gobsmacked.

Figure 7. Average of all of the pseudoproxies after simply flipping over (inverting) those with a negative correlation with the instrumental data.
YOICKS!
Here, we can see why all the different averaging methods yield the same “historical record” … because the procedure listed above actively mines for hockeysticks in random red noise.
One interesting detail of Figure 7 is that there is a sharp drop in the average before the start of the period used for the correlation. I assume this is because to get that large an increase, you need to first go down to a low point.
And this dip prior to 1850 is of interest because you can see it in both Panel A and Panel B of the PAGES2K reconstructions shown in Figure 3 above …
Another item of note is that the procedure has introduced a slight downward trend from the beginning to a sharp drop around 1775. I ascribe that to the procedure favoring “U” shaped datasets, but hey, that’s just me.
In any case, the slight downward trend is a real effect of the procedure. We know that because there’s no downward trend in the full dataset. We also know it’s a real effect for a more important reason—we see the same slight downward trend in the original MBH Hockeystick in Fig.1, and also in Panel “a” of Figure 2.
Finally, why is there so little variation in the “handle” of the hockeystick? Are the temperatures of the past really that stable?
Nope. It’s another artifact. The handle of the hockeystick is just an average of some presumably large number of random red noise datasets. When you average a bunch of random red noise datasets, you get a straight line.
Moving along, my next thought was, how much do I have to disturb the pseudoproxies in order to produce a visible hockeystick?
To investigate that, I took the same original dataset. In this case, however, I inverted only 40 proxies, the ones with the greatest negative correlation. So I was flipping only the strongest negative signals, and leaving the rest of the proxies that had negative correlation as untouched red noise. Here’s that result.

Figure 8. Average of all of the pseudoproxies after flipping over those with the top forty negative correlation with the instrumental data.
Note that less than six percent (forty) of the pseudoproxies were flipped, and all four hockeystick characteristics are already visible—reduced variation in the “handle” of the hockeystick, a slight downward trend to 1775, a sharp drop to 1850, and a nearly vertical hockeystick “blade” from 1850 on.
How about at the other end, where we select only the ones with the strongest correlation? Here’s the average of only the top quarter of the data (176 pseudoproxies) as measured by their correlation with the observational temperature.

Figure 8. Average of only the top quarter of the data, those with the best correlation with Berkeley Earth data.
Same thing. Straight handle on the hockeystick. Slow decline to 1775. Sharp drop. Vertical hockeystick blade after that.
Finally, after sleeping on it, I realized I’d looked at the best-case scenarios … but what about the worst-case? So here’s the half of the pseudoproxies with the worst correlation with the observational temperature.

Figure 9. Average of only the bottom half of the data, those with the worst correlation with Berkeley Earth data.
Despite using only the half of the pseudoproxies with the poorest correlation with temperatures, those with a correlation of 0.22 or less, we get the same story as before—same straight hockeystick handle, same slight drop to 1775, same sharp drop to 1850, and the same vertical hockeystick blade after 1850.
Now, there’s an interesting and easily missed point in the graphics above. While the shape stays the same, the greater the correlation, the taller the blade of the hockeystick. The different procedures changed the tip of the blade from ~0.1 with only 40 flipped, to ~1.5 using the worst-correlated pseudoproxies, to ~0.3 with all pseudoproxies flipped, to around ~0.7 using only the best correlated. So all of them showed the identical “hockeystick” form, and they only varied in the size of the blade. Curious.
Now I stated up above that this post would show why it is both true and meaningless that various studies all come up with hockeysticks.
The reason is quite evident in the figures above—no matter what the investigators do, since they are all using some variation of the standard procedure I listed at the top of the post, they are guaranteed to get a hockeystick. Can’t escape it. That procedure definitely and very effectively mines hockeysticks out of random red noise.
Here, it’s an irenic long summer evening, with bursts of childrens’ laughter radiating out of the open windows. I have the great joy of living with my gorgeous ex-fiance, our daughter and her husband, a granddaughter who is “almost five, Papa!” and a grandson heading towards three.
Is there a lovelier sound than their laughter?
Best to all,
w.
The Usual: When you comment please quote the exact words you are discussing. I can defend my words, but I can’t defend your interpretation of my words. And if you want to show I’m wrong, see How To Show Willis Is Wrong.
Related